L’arithmétique est une partie des mathématiques qui s’intéresse aux nombres entiers. Nous les manipulons depuis notre plus jeune âge et pourtant, ces nombres si naturels dissimulent des propriétés insoupçonnées, parfois non encore prouvées. Parmi tous ces nombres figurent les nombres premiers, à l’origine de tous les autres. Leur connaissance est à la fois précieuse en mathématiques comme dans notre vie quotidienne …
En jouant avec deux dès, nous avons découvert qu’une situation aléatoire, dépendante du hasard, pouvait être étudiée mathématiquement. Il ne s’agit pas de prévoir le hasard mais de calculer des probabilités, c’est à dire de mesurer la « chance » qu’un évènement se produise, sur le nombre de résultats possibles. Cette branche des mathématiques s’appelle les probabilités.
Une fonction peut s’exprimer à l’aide d’une formule littérale et se représenter par un graphique. Un cas simple de graphique est la droite. A quel type de fonction peut-on l’associer ? Souvenons-nous … une situation de proportionnalité se caractérise par une droite passant par l’origine. Nous parlerons de fonction linéaire. Si la droite ne passe pas par l’origine, son décalage vertical se retrouve dans la formule littérale associée. Nous parlerons de fonction affine.
Comment retrouver la hauteur d’une pyramide Egyptienne, découverte en 2013 mais réduite à sa base carrée et à quelques pierres de parement ? L’idée est simple et repose sur le fait qu’une mesure angulaire est invariante, par réduction ou agrandissement. Mais l’existence de coefficients multiplicatifs constants reliant les côtés de triangles rectangles semblables permet de déterminer cette hauteur, par le calcul et de manière précise. C’est l’objet de la trigonométrie qui s’intéresse aux relations entre les longueurs et les angles dans les triangles.
A la différence des probabilités, les statistiques s’intéressent à observer des phénomènes concrets. Le travail du statisticien consiste alors à collecter des données, à les traiter, les analyser, les interpréter et les présenter afin de les rendre compréhensibles par tous. Les statistiques sont à la fois une science, une méthode et un ensemble de techniques.
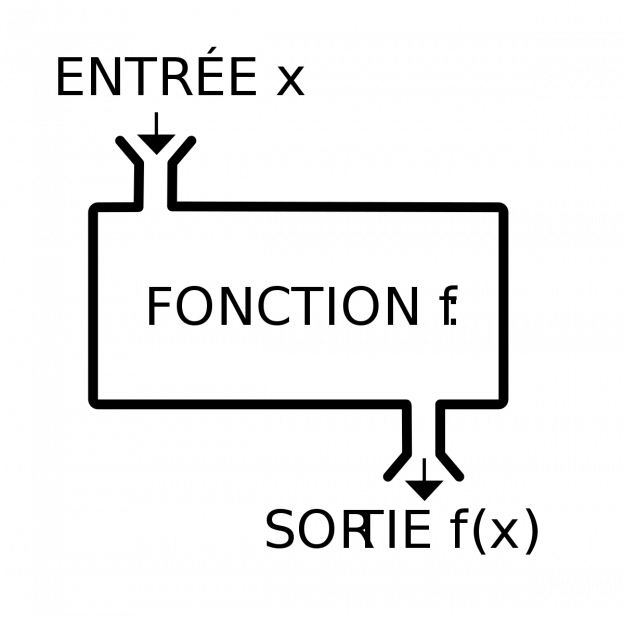
L’étude d’un phénomène physique nécessite souvent de s’intéresser à l’évolution d’une grandeur numérique par rapport à une autre, de manière expérimentale ou à l’aide d’une formule théorique. Le recours à un tableau de données ou à un graphique permet de mieux visualiser le comportement de la grandeur étudiée, dite « de sortie » en fonction d’une grandeur variable dite « d’entrée ». Ce procédé qui met en relation ces deux grandeurs est appelé « fonction numérique ».
Nous reprenons l’étude d’expressions littérales et nous nous intéressons à la factorisation, processus contraire de l’action de développer. Nous découvrons deux méthodes de factorisation et appliquons celles-ci à la résolution d’équations dites « produit nul ».
La Terre est sphérique … enfin presque ! Son étude nous amène à comprendre comment se repérer sur sa surface, à l’aide des coordonnées géographiques. Ses caractéristiques numériques sont l’occasion d’apprendre les formules de l’aire d’une sphère et du volume d’une boule.